Конгруэнтно это: Конгруэнтность. Что такое «Конгруэнтность»? Понятие и определение термина «Конгруэнтность» – Глоссарий
Конгруэнтно Или Неконгруэнтно | Невербалика
Из статьи вы узнаете: - Конгруэнтно - это как? Или почему ложь - это двойное послание? - Почему невербалику сложно контролировать?
Конгруэнтно и неконгруэнтно, где грань. Или ложь – это всегда двойное послание.
Конгруэнтно, конгруэнтность (от англ. congruence) – подлинность, открытость, честность. Одно из “необходимых и достаточных условий” как эффективного психотерапевтического контакта, так и отношений. Наряду с эмпатией и безоценочным позитивным принятием.
Термин “конгруэнтно”.
Термин “конгруэнтность” введен в психологию К.Роджерсом. С какой целью? Для описания соответствия “идеального я”, “я” и “опыта” в жизни человека. Плюс для динамического состояния психотерапевта. В котором различные элементы его внутреннего опыта (эмоции, чувства, установки, переживания) адекватно, неискаженно и свободно проживаются, осознаются и выражаются в ходе работы с клиентом.
Конгруэнтное поведение, выражающее внутренние состояния и стремления, несет с собой переживания целостности, достоинства, комфорта. Это заметно со стороны по невербальным проявлениям. Согласованности слов, действий и мимики, жестов, интонаций, тембра голоса, гармоничности движений и их адекватности ситуации. Часто степень конгруэнтности партнера по общению оценивается интуитивно и неосознанно.
Неконгруэнтность выражает себя в несоответствии между невербальными и вербальными компонентами поведения. Вы можете наблюдать, видеть и слышать ее. Например, в общении с клиентом по разным каналам восприятия. Обращайте внимание на речь, интонацию голоса, позу, жесты, мимику, – на рассогласованность сообщений. Как будто с вами одновременно об одном и том же разговаривают несколько, противоречащих друг другу собеседников. Неконгруэнтность – оговорки, неполная сосредоточенность на желаемом результате, внутренний конфликт, выражающийся в поведении.
Вербальные и невербальные сигналы могут выдавать два противоречивых сообщения.
Как мы реагируем на противоречивые сигналы:
1. Первая реакция “провал”, “подвисание”, неопределенность, сомнение.
2. Затем мы стараемся получить более полную информацию.
3. Если нам что-то не удается прояснить, мы реагируем негативно, внутренне отказываемся продолжать общение.
И когда налицо два сигнала, которые противоречат друг другу, мы доверяем тем, которые труднее всего подделать. Верификаторы знают, что труднее всего подделать невербальное поведение, нежели слова.
Когда человек говорит неправду, то он неконгруэнтен. Как результат, транслирует двойное послание. Слова говорят неправду, а невербалика (тело, лицо, жесты) противоречат словам и несут истинную информацию. Если, конечно, вы не супер разведчик, когорого готовили годами.
Основная задача верификатора научиться видеть и распознавать двойное послание лжеца.
Подробно этой темой занимаемся на курсе по распознаванию лжи.
Профайлер Верификатор практик
4 причины, по которым невербалику сложно контролировать.
Существуют главные четыре причины того, почему невербальное поведение сложнее контролировать, чем вербальное.
– Есть рефлекторные связи между эмоциями и невербальным поведением. Тогда как аналогичных связей между эмоциями и речью нет. Например, когда человек пугается, он автоматически отклоняется назад, и на его лице появляется определенное выражение.
Однако, нет такой определенной фразы или речевого оборота, которую человек всегда непроизвольно произносит в момент страха.
Представьте себе девочку. Она смотрит телевизор вместо того, чтобы делать домашнее задание. Когда ее отец входит в комнату, она говорит ему, что только что закончила уроки. Сказав это, она пугается, так как понимает, что он может захотеть проверить ее.

Чтобы не показать свой страх, она вынуждена как-то перебороть рефлекторные невербальные реакции. Ведь они неразрывно связаны со страхом. В то же время ей не нужно беспокоиться о вербальной реакции, она не автоматическая.
– Большинство людей лучше подготовлены в использовании слов, нежели в управлении поведением. Так как они, как правило, считают, что речь более важна в обмене информацией, чем поведение.
Если вы попросите что-то рассказать, ваш собеседник будет пользоваться словами. С их помощью он будет кодировать свой опыт и доносить его до вас. Жестов будет не так много, как слов. Исключение, правда, составят люди гипертимного характера 😉
Язык глухонемых в данном случае не является исключением, поскольку он в данном контексте заменяет отдельные слова, символы и буквы.
– Общепринятый социальный факт, что слова в обмене информацией важнее поведения. Он заставляет людей обращать больше внимания на то, что они говорят. И в меньшей степени на то, что они делают. Оратор наверняка помнит, что он сказал во время своей презентации. Но свою «невербалику» он вряд ли воспроизведет также точно, как содержание выступления.
И в меньшей степени на то, что они делают. Оратор наверняка помнит, что он сказал во время своей презентации. Но свою «невербалику» он вряд ли воспроизведет также точно, как содержание выступления.
– Человек не может молчать или врать на невербальном уровне. Предположим, человек что-то скрывает. Он пытается это утаить от окружающих усилием воли. Видна будет не та информация, которую он скрывает, а те усилия, которые он предпринимает для ее сокрытия. Мы получим неконгруэнтное поведение или “утечки”. А это один из главных признаков того, что человек лжет. И напротив, конгруэнтно – это когда тело и невербальное поведение не противоречат тому, что человек говорит.
Конгруэнтно или неконгруэнтно – вот главный вопрос. Невербальное поведение, с учетом трудностей его контролирования, являться очень ценным источником информации при выявлении лжи говорящего.
Профайлер верификатор практик
микроструктура определяет свойства — Научно-исследовательский портал Уральского федерального университета
Проект: Проект-Грант
Проект нацелен на решение задач структурообразования в конгруэнтно плавящихся сплавах Al50Ni50, Cu50Zr50, Ni50Zr50, относящихся к стеклообразующим материалам (глассформерам), часто образующих интерметаллидные фазы и применяемых в качестве материалов с повышенными механическими свойствами, а также контактных материалов для коммутации сильных токов.
Аналитическими методами и методами компьютерного моделирования с анализом и количественным описанием получаемых экспериментальных данных планируется изучение механизмов дендритного роста в переохлаждённых расплавах, формирование зеренной структуры, исследование влияния микроструктуры на свойства конгруэнтно плавящихся металлических глассформеров. Для этого будет использован объединяющий подход теории фазовых переходов Л.Д. Ландау для описания задач многомасштабного математического моделирования структурообразования в бинарных глассформерах. Будет сформулирована общая методология, основанная на формулировке энтропийного функционала или функционала свободной энергии, учитывающего особенности поведения сплава при его плавлении и затвердевании. Будет получена единая система уравнений, пригодных для моделирования как медленных процессов переноса и фазовых превращений (лимитируемых атомной диффузией, кондуктивным или конвективным переносом тепла и атомных / кластерных компонентов сплава), так и сверхскоростных фазовых переходов, скорость протекания которых сопоставима со скоростью локальной термализации сплава, атомной диффузии или скоростью локальной структурной релаксации.

 Информация о параметрах, полученная на микроуровне [с помощью модели Кристаллического Фазового Поля (КФП-модели)], будет передаваться на мезоскопический уровень (для задач, основанных на модели дендритного роста стефановского типа и модели фазового поля для расчета дендритов и зерен). Результаты мезоскопического моделирования будут затем проанализированы по отношению к механическим свойствам (Al50Ni50) и переданы на макроскопический уровень (с учетом моделирования по теории двухфазной зоны) для оценки электрических параметров сплавов Zr50Cu50 и Ni50Zr50 в зависимости от зеренного строения и фазового состава. В результате, кинетика дендритной и зеренной кристаллизации в конгруэнтно плавящихся глассформерах (т.е. в стеклообразующих сплавах) может быть промоделирована с помощью метода совмещенного анализа, основанного на использовании экспериментальных данных (например, температурной зависимости вязкости расплава), данных атомистического моделирования (по выявлению температурной зависимости формирования кластерной структуры жидкости, цепочек кластеров и сеток этих цепочек) и мезоскопической модели дендритной кристаллизации.
Информация о параметрах, полученная на микроуровне [с помощью модели Кристаллического Фазового Поля (КФП-модели)], будет передаваться на мезоскопический уровень (для задач, основанных на модели дендритного роста стефановского типа и модели фазового поля для расчета дендритов и зерен). Результаты мезоскопического моделирования будут затем проанализированы по отношению к механическим свойствам (Al50Ni50) и переданы на макроскопический уровень (с учетом моделирования по теории двухфазной зоны) для оценки электрических параметров сплавов Zr50Cu50 и Ni50Zr50 в зависимости от зеренного строения и фазового состава. В результате, кинетика дендритной и зеренной кристаллизации в конгруэнтно плавящихся глассформерах (т.е. в стеклообразующих сплавах) может быть промоделирована с помощью метода совмещенного анализа, основанного на использовании экспериментальных данных (например, температурной зависимости вязкости расплава), данных атомистического моделирования (по выявлению температурной зависимости формирования кластерной структуры жидкости, цепочек кластеров и сеток этих цепочек) и мезоскопической модели дендритной кристаллизации.
Особое внимание будет уделяться анализу влияния скорости охлаждения, переохлаждения и конвекции на формирование дендритно-зеренной структуры конгруэнтно плавящихся сплавов. В частности, скорость охлаждения позволит оценить возможность появления метастабильных фаз (которые, как правило, могут обладать существенно лучшими механическими и электрическими свойствами сплавов). В качестве исследования влияния управляющих параметров на формирование микроструктуры также будут рассмотрены два типа конвективных течений в расплавах: (i) естественная конвекция, вызванная гравитационным полем и температурным градиентом, который связан с выделением скрытой теплоты фазового превращения на межфазной поверхности дендритных структур (важный случай применения электростатического левитатора для обработки и получения образцов) и (ii) вынужденная конвекция, вызванная термоэлектрическим и магнитогидродинамическим эффектами в левитируемых материалах (важный случай применения электромагнитного левитатора для обработки и получения образцов, а также лазерной и электронной перекристаллизации поверхностных слоёв металлических сплавов).

Проект объединяет ряд актуальных фундаментальных задач, решение которых может быть выполнено аналитическими методами (в простейших случаях динамики фазовых переходов в виде бегущих волн), а также развиваемого в проекте программного комплекса, включающего распараллеливание разработанных градиентно-устойчивых алгоритмов и программ решения сформулированных в проекте задач. Для численного решения подобной системы уравнений и частных задач проекта предлагается использование метода фазового поля (для описания формирования кристаллических зерен на пространственном мезоуровне) и метода кристаллического фазового поля (для описания формирования нанозерен на пространственном микроуровне) с применением градиентно-безусловно устойчивых алгоритмов. Безусловная устойчивость алгоритма означает непрерывное убывание свободной энергии системы во времени при сохранении численной устойчивости и использования произвольного соотношения пространственно-временного дискретизирования уравнений фазового поля.

| Активный | |
| Действительная дата начала/окончания | 19/04/2021 → 31/12/2023 |
Смотреть все
Смотреть меньше
- 29.
 19.15 Фазовые равновесия и фазовые переходы
19.15 Фазовые равновесия и фазовые переходы
- НИЧ Куйбышева
Atomistic-informed kinetic phase-field modeling of non-equilibrium crystal growth during rapid solidification
Kavousi, S., Ankudinov, V., Galenko, P. K. & Asle Zaeem, M., 1 июл. 2023, В: Acta Materialia. 253, 118960.Результат исследований: Вклад в журнал › Статья › рецензирование
Открытый доступ
Anomalous Dynamics of Recalescence Front in Crystal Growth Processes: Theoretical Background
Alexandrov, D. V., Galenko, P. K. & Toropova, L. V., 2022, В: Crystals. 12, 12, 1686.
V., Galenko, P. K. & Toropova, L. V., 2022, В: Crystals. 12, 12, 1686.Результат исследований: Вклад в журнал › Статья › рецензирование
Anomalous kinetics, patterns formation in recalescence, and final microstructure of rapidly solidified Al-rich Al-Ni alloys
Galenko, P. K., Toropova, L. V., Alexandrov, D. V., Phanikumar, G., Assadi, H., Reinartz, M., Paul, P., Fang, Y. & Lippmann, S., дек. 2022, В: Acta Materialia. 241, 118384.
K., Toropova, L. V., Alexandrov, D. V., Phanikumar, G., Assadi, H., Reinartz, M., Paul, P., Fang, Y. & Lippmann, S., дек. 2022, В: Acta Materialia. 241, 118384.Результат исследований: Вклад в журнал › Статья › рецензирование
Открытый доступ
A Stable Mode of Dendritic Growth in Cases of Conductive and Convective Heat and Mass Transfer
Toropova, L. V., Galenko, P. K. & Alexandrov, D. V., июл. 2022, В: Crystals. 12, 7, 965.
V., Galenko, P. K. & Alexandrov, D. V., июл. 2022, В: Crystals. 12, 7, 965.Результат исследований: Вклад в журнал › Обзорная статья › рецензирование
Открытый доступ
1 Цитирования (Scopus)
Что конгруэнтно ⭐ Определение, формулы, факты, примеры
- Дом
- >
- База знаний
- >
- Конгруэнтность — определение с примерами
Добро пожаловать в Brighterly, где мы делаем математику веселой и легкой для детей! Сегодня мы узнаем о конгруэнтности треугольников. Конгруэнтные треугольники — важное понятие в геометрии, и их понимание поможет вам решить многие математические задачи. Давайте начнем!
Конгруэнтные треугольники — важное понятие в геометрии, и их понимание поможет вам решить многие математические задачи. Давайте начнем!
Конгруэнтное значение в математике
В математике конгруэнтные объекты имеют одинаковый размер и форму. Термин «конгруэнтность» происходит от латинского слова «congruere», что означает «собираться вместе». С математической точки зрения это означает, что два объекта идеально подходят друг другу, как две части головоломки. Например, если у нас есть два конгруэнтных треугольника, мы можем сказать, что все их стороны и углы равны, и они имеют одинаковый размер и форму.
Конгруэнтность имеет различные применения в различных областях математики, таких как геометрия, алгебра и тригонометрия. В геометрии конгруэнтность используется для определения конгруэнтных фигур, которые представляют собой фигуры, идентичные по размеру и форме. В алгебре конгруэнтность используется для определения конгруэнтных чисел, которые представляют собой целые числа, имеющие одинаковый остаток при делении на заданный модуль.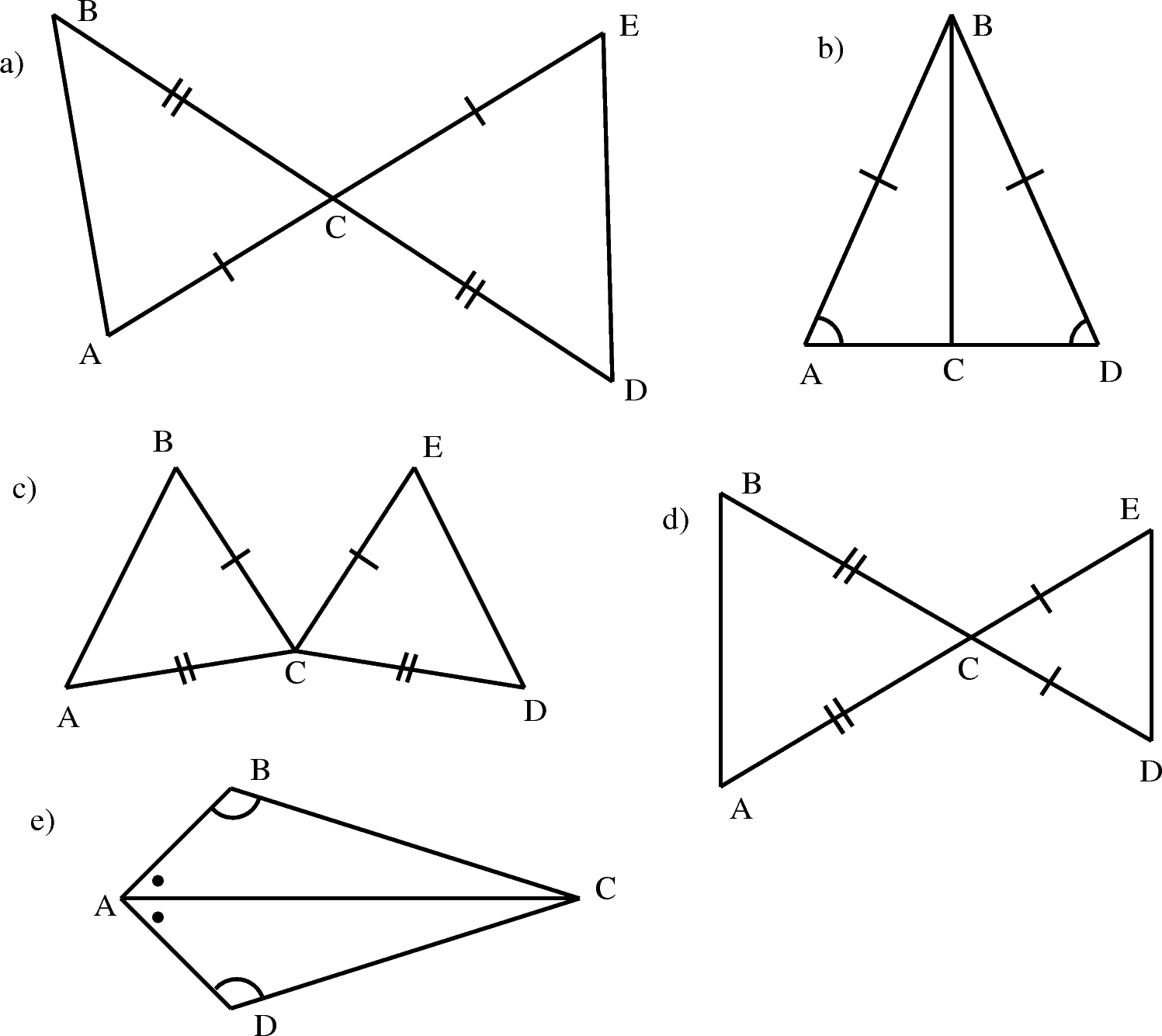 В тригонометрии конгруэнтность используется для определения конгруэнтных треугольников, которые имеют одинаковый размер и форму.
В тригонометрии конгруэнтность используется для определения конгруэнтных треугольников, которые имеют одинаковый размер и форму.
Конгруэнтное значение в геометрии
В геометрии конгруэнтные фигуры — это формы, которые могут быть преобразованы друг в друга посредством вращения, отражения или перемещения. Эти преобразования не меняют размер или форму фигур, поэтому они остаются конгруэнтными даже после перемещения или переворачивания. Другими словами, конгруэнтные фигуры имеют одинаковый размер и форму, но могут находиться в разных положениях или ориентациях.
Понятие конгруэнтности имеет важное значение в геометрии, поскольку оно помогает определить многие геометрические фигуры и их свойства. Например, конгруэнтные отрезки — это отрезки одинаковой длины, а конгруэнтные углы — это углы, имеющие одинаковую меру. Конгруэнтные окружности — это окружности с одинаковым радиусом, а конгруэнтные треугольники — это треугольники с одинаковыми размером и формой.
Рабочие листы по геометрии Конгруэнтные треугольники
Конгруэнтные треугольники. Ответы на рабочем листе
Ответы на рабочем листе
Символ конгруэнтности
Символ конгруэнтности «≅», представляющий собой комбинацию двух параллельных линий. Например, если у нас есть два конгруэнтных треугольника, мы можем записать это как △ABC ≅ △DEF. Это обозначение говорит нам, что треугольник ABC конгруэнтен треугольнику DEF.
Конгруэнтные отрезки, углы, окружности и треугольники
Конгруэнтные отрезки — это отрезки одинаковой длины. Мы можем обозначить это, написав AB ≅ CD, что означает, что отрезок AB конгруэнтен отрезку CD. Конгруэнтные углы — это углы, которые имеют одинаковую меру в градусах. Мы можем записать это как ∠A ≅ ∠B, что означает, что угол A конгруэнтен углу B. Конгруэнтные окружности — это окружности, имеющие одинаковый радиус. Мы можем записать это как ⊙A ≅ ⊙B, что означает, что окружность A конгруэнтна окружности B.
Конгруэнтные треугольники — это треугольники одинакового размера и формы. Два треугольника равны, если все их соответствующие стороны и углы равны. Существует четыре основных постулата или правила для определения конгруэнтности двух треугольников: SSS, SAS, ASA и AAS.
Существует четыре основных постулата или правила для определения конгруэнтности двух треугольников: SSS, SAS, ASA и AAS.
В SSS (Side-Side-Side), если все три стороны одного треугольника конгруэнтны соответствующим сторонам другого треугольника, то треугольники конгруэнтны. В SAS (сторона-угол-сторона), если две стороны и угол между ними одного треугольника конгруэнтны соответствующим сторонам и углу между ними другого треугольника, то треугольники конгруэнтны. В ASA (угол-сторона-угол), если два угла и прилежащая к ним сторона одного треугольника конгруэнтны соответствующим углам и прилежащей к ним стороне другого треугольника, то треугольники конгруэнтны. В AAS (угол-угол-сторона), если два угла и невключенная сторона одного треугольника конгруэнтны соответствующим углам и невключенной стороне другого треугольника, то треугольники конгруэнтны.
Разница между конгруэнтными фигурами и подобными фигурами
Хотя конгруэнтные фигуры имеют одинаковый размер и форму, похожие фигуры имеют одинаковую форму, но не обязательно одинаковый размер. Думайте о похожих фигурах как о масштабных версиях друг друга, как о уменьшенной или увеличенной копии одной и той же картинки. Другими словами, две фигуры подобны, если они имеют одинаковую форму, но не обязательно одинаковый размер.
CPCT Математические правила
CPCT расшифровывается как «Соответствующие части конгруэнтных треугольников». Это означает, что если два треугольника равны, то их соответствующие части (стороны и углы) также равны. Это свойство полезно при решении задач, связанных с конгруэнтными треугольниками.
Решенные примеры
Давайте рассмотрим несколько решенных примеров, чтобы лучше понять концепцию конгруэнтных треугольников.
Пример 1: В треугольнике ABC AB = 4 см, BC = 6 см и AC = 8 см. В треугольнике DEF DE = 4 см, EF = 6 см и DF = 8 см. Два треугольника равны?
Два треугольника равны?
Решение: Мы можем использовать постулат SSS, чтобы проверить конгруэнтность треугольников. Поскольку AB = DE, BC = EF и AC = DF, мы можем заключить, что эти два треугольника конгруэнтны.
Пример 2: В треугольнике PQR PQ = 5 см, QR = 7 см и RP = 6 см. В треугольнике XYZ XY = 8 см, YZ = 10 см и ZX = 6 см. Два треугольника равны?
Решение: Мы можем использовать постулат SAS, чтобы проверить конгруэнтность треугольников. Поскольку PQ = XY, RP = XZ и ∠PQR = ∠XYZ, мы можем заключить, что эти два треугольника конгруэнтны.
Практические задачи
Теперь, когда мы рассмотрели несколько примеров, пришло время попрактиковаться самостоятельно! Попробуйте решить эти задачи, чтобы проверить свое понимание конгруэнтных треугольников.
В треугольнике ABC AB = 6 см, BC = 8 см и AC = 10 см. В треугольнике DEF DE = 5 см, EF = 7 см и DF = 9см. Два треугольника равны? Если да, то какой постулат вы использовали?
В треугольнике LMN LM = 12 см, MN = 10 см и NL = 8 см.
 В треугольнике XYZ XY = 16 см, YZ = 13 см и ZX = 10 см. Два треугольника равны? Если да, то какой постулат вы использовали?
В треугольнике XYZ XY = 16 см, YZ = 13 см и ZX = 10 см. Два треугольника равны? Если да, то какой постулат вы использовали?В треугольнике PQR PQ = 9 см, QR = 12 см и RP = 15 см. В треугольнике STU ST = 6 см, TU = 8 см и US = 10 см. Два треугольника равны? Если да, то какой постулат вы использовали?
Заключение
Конгруэнтные треугольники — важное понятие в геометрии, и их понимание может помочь вам решить многие математические задачи. Помните, что два треугольника равны, если все их соответствующие стороны и углы равны. Существует четыре основных постулата для определения конгруэнтности двух треугольников: SSS, SAS, ASA и AAS. Продолжайте практиковаться, и вы быстро станете профессионалом в построении конгруэнтных треугольников!
Часто задаваемые вопросы о конгруэнтности
Что означает CPCT в математике?
CPCT расшифровывается как «Соответствующие части конгруэнтных треугольников». Когда два треугольника конгруэнтны, их соответствующие части (стороны, углы, вершины) также конгруэнтны. Это фундаментальное понятие в геометрии, которое позволяет нам сравнивать и анализировать различные части конгруэнтных треугольников. Правило CPCT часто используется при решении задач, связанных с конгруэнтными треугольниками, поскольку оно обеспечивает быстрый способ определения соответствующих конгруэнтных частей.
Это фундаментальное понятие в геометрии, которое позволяет нам сравнивать и анализировать различные части конгруэнтных треугольников. Правило CPCT часто используется при решении задач, связанных с конгруэнтными треугольниками, поскольку оно обеспечивает быстрый способ определения соответствующих конгруэнтных частей.
Какие четыре постулата используются для определения конгруэнтности двух треугольников?
Четыре постулата или правила для определения конгруэнтности двух треугольников:
SSS (Side-Side-Side): если все три стороны одного треугольника конгруэнтны соответствующим сторонам другого треугольника, то треугольники конгруэнтны.
SAS (сторона-угол-сторона): если две стороны и угол между ними одного треугольника конгруэнтны соответствующим сторонам и углу между ними другого треугольника, то треугольники конгруэнтны.
ASA (Угол-Сторона-Угол): Если два угла и прилежащая к ним сторона одного треугольника конгруэнтны соответствующим углам и прилежащей к ним стороне другого треугольника, то треугольники конгруэнтны.

AAS (Угол-Угол-Сторона): Если два угла и не включенная в них сторона одного треугольника конгруэнтны соответствующим углам и не входящей стороне другого треугольника, то треугольники конгруэнтны.
Эти постулаты используются для доказательства конгруэнтности двух треугольников, и они основаны на том факте, что соответствующие стороны и углы конгруэнтных треугольников равны.
В чем разница между конгруэнтными и подобными фигурами?
Конгруэнтные фигуры — это фигуры, имеющие одинаковый размер и форму. Две фигуры равны, если все их соответствующие стороны и углы равны. Конгруэнтные фигуры могут быть преобразованы друг в друга путем вращения, отражения или перемещения без изменения их размера или формы. Подобные фигуры, напротив, имеют одинаковую форму, но могут различаться по размеру. Две фигуры подобны, если они имеют одинаковую форму, но их соответствующие стороны пропорциональны. Другими словами, одна фигура представляет собой масштабированную версию другой. Понятие подобия часто используется в геометрии для сравнения форм различных объектов.
Понятие подобия часто используется в геометрии для сравнения форм различных объектов.
Что означает конгруэнтность?
Символ конгруэнтности «≅» представляет собой комбинацию двух параллельных линий. Этот символ используется для обозначения того, что две геометрические фигуры конгруэнтны, то есть имеют одинаковый размер и форму. Например, если у нас есть два конгруэнтных треугольника, мы можем записать это как △ABC ≅ △DEF. Это говорит нам о том, что треугольник ABC равен треугольнику DEF.
Почему конгруэнтность важна в геометрии?
Конгруэнтность важна в геометрии, потому что она помогает определить многие геометрические фигуры и их свойства. Конгруэнтные фигуры имеют одинаковый размер и форму, что позволяет точно измерять и анализировать геометрические свойства. Идентифицируя соответствующие части конгруэнтных треугольников, мы можем сравнивать и анализировать различные части геометрических фигур. Конгруэнтность также используется в геометрии для решения задач, связанных с углами, сторонами и другими геометрическими свойствами фигур. Кроме того, понятие конгруэнтности лежит в основе многих геометрических теорем и доказательств.
Кроме того, понятие конгруэнтности лежит в основе многих геометрических теорем и доказательств.
- Математический стек Exchange
- Brilliant Wiki: конгруэнтные треугольники
- Википедия
Конгруэнтность: определения и примеры — Club Z! Репетиторство
Конгруэнтность — это математический термин, обозначающий равенство двух форм или объектов с точки зрения их размера и формы. Проще говоря, конгруэнтность означает, что два объекта идентичны друг другу с точки зрения их формы и размера, хотя они могут быть по-разному ориентированы в пространстве. Эта концепция важна в различных областях математики, включая геометрию, тригонометрию и алгебру.
Конгруэнтность можно применять к двухмерным формам, таким как треугольники, круги и прямоугольники, а также к трехмерным объектам, таким как кубы и сферы. В геометрии две фигуры называются конгруэнтными, если они имеют одинаковый размер и форму и если одна форма может быть преобразована в другую с помощью ряда жестких движений. Жесткие движения включают переводы, вращения и отражения.
Жесткие движения включают переводы, вращения и отражения.
Когда две фигуры конгруэнтны, они имеют одинаковую площадь, периметр и углы. Например, если два треугольника конгруэнтны, их соответствующие стороны и углы равны по длине и величине. Другими словами, два треугольника имеют одинаковую форму и размер, и один из них можно наложить на другой.
Концепция конгруэнтности важна во многих областях математики, включая тригонометрию, где конгруэнтные углы используются для доказательства теорем и решения задач. Например, в прямоугольном треугольнике два острых угла равны, что означает, что они имеют одинаковую меру. Это позволяет нам использовать тригонометрические функции для нахождения длин сторон треугольника или для решения неизвестных углов.
В алгебре конгруэнтность используется для описания отношений между числами. Два числа называются равными, если они имеют одинаковый остаток при делении на определенное число. Например, если два числа конгруэнтны по модулю 5, это означает, что они имеют одинаковый остаток при делении на 5. В этом случае мы можем записать конгруэнтность следующим образом:
В этом случае мы можем записать конгруэнтность следующим образом:
а ? b (mod 5)
Это обозначение означает, что a и b конгруэнтны по модулю 5. Конгруэнтность по модулю n является важным понятием в теории чисел, изучающей свойства целых чисел.
Конгруэнтность также может использоваться для описания свойств форм и фигур. Например, правильный многоугольник — это многоугольник, у которого все стороны и углы равны. Это означает, что все стороны многоугольника имеют одинаковую длину и все углы имеют одинаковую меру. Например, правильный шестиугольник имеет шесть сторон одинаковой длины и шесть углов по 120 градусов каждый.
В дополнение к правильным многоугольникам существуют другие типы фигур, обладающие конгруэнтными свойствами. Например, конгруэнтные окружности — это окружности с одинаковым радиусом и, следовательно, с одинаковой длиной окружности и площадью. Конгруэнтные прямоугольники — это прямоугольники, имеющие одинаковую длину и ширину, а значит, одинаковый периметр и площадь.
В геометрии сравнение часто используется для доказательства теорем и решения задач. Например, если два треугольника конгруэнтны, мы можем использовать этот факт, чтобы доказать, что некоторые углы или стороны равны. Это известно как теорема о конгруэнтности, которая утверждает, что два треугольника конгруэнтны тогда и только тогда, когда их соответствующие стороны и углы равны.
Конгруэнтность также можно использовать для решения проблем в реальных ситуациях. Например, если два треугольника конгруэнтны, мы можем использовать этот факт для определения расстояния между двумя точками в пространстве. Это известно как теорема Пифагора, которая утверждает, что в прямоугольном треугольнике сумма квадратов двух катетов равна квадрату гипотенузы.
В заключение, конгруэнтность относится к объектам или формам, которые имеют одинаковый размер и форму. Это важное понятие в математике и геометрии, так как оно помогает нам определить, когда две формы идентичны и когда они могут быть преобразованы друг в друга путем перемещения, вращения или отражения. Конгруэнтность также используется в различных областях, таких как инженерия, архитектура и физика, для обеспечения точности и точности проектирования и измерений. Понимание конгруэнтности важно для всех, кто изучает математику или любую другую область, связанную с геометрическими понятиями, поскольку оно обеспечивает основу для более сложных понятий, таких как сходство, симметрия и преобразования.
Конгруэнтность также используется в различных областях, таких как инженерия, архитектура и физика, для обеспечения точности и точности проектирования и измерений. Понимание конгруэнтности важно для всех, кто изучает математику или любую другую область, связанную с геометрическими понятиями, поскольку оно обеспечивает основу для более сложных понятий, таких как сходство, симметрия и преобразования.
Определение конгруэнтности
В математике конгруэнтными фигурами называются две или более фигуры, идентичные по форме и размеру. Термин «конгруэнтность» происходит от латинского слова «congruere», что означает «согласовывать» или «соответствовать». Конгруэнтные фигуры имеют одинаковые размеры, углы и меры, поэтому их можно накладывать друг на друга путем переноса, поворота или отражения.
Конгруэнтные фигуры можно использовать для решения множества математических задач. Они используются в геометрии для определения соответствующих сторон и углов, для доказательства теорем и решения уравнений. Конгруэнтные фигуры также можно использовать в тригонометрии, алгебре и исчислении.
Конгруэнтные фигуры также можно использовать в тригонометрии, алгебре и исчислении.
Пример 1: конгруэнтные треугольники
Одним из наиболее распространенных примеров конгруэнтных фигур является конгруэнтный треугольник. Два треугольника равны, если они имеют одинаковую форму и размер. Это означает, что их соответствующие стороны и углы равны по размеру.
Например, если треугольник ABC равен треугольнику DEF, это означает, что:
- Длина стороны AB равна длине стороны DE
- Длина стороны AC равна длине стороны DF
- Длина стороны BC равна длине стороны EF
- Угол А равен углу D
- Угол B равен углу E
- Угол C равен углу F
Пример 2: конгруэнтные прямоугольники
Другим примером конгруэнтных фигур является конгруэнтный прямоугольник. Два прямоугольника равны, если они имеют одинаковую форму и размер. Это означает, что их соответствующие стороны и углы равны по размеру.
Например, если прямоугольник PQRS равен прямоугольнику WXYZ, это означает, что:
- Длина стороны PQ равна длине стороны WX
- Длина стороны QR равна длине стороны YZ
- Длина стороны PS равна длине стороны WZ
- Длина стороны RS равна длине стороны XY
- Угол P равен углу W
- Угол Q равен углу X
- Угол R равен углу Y
- Угол S равен углу Z
Пример 3: конгруэнтные окружности
Третий пример конгруэнтных фигур — конгруэнтный круг. Две окружности конгруэнтны, если они имеют одинаковый радиус. Это означает, что их соответствующие точки на окружности равноудалены от центра.
Две окружности конгруэнтны, если они имеют одинаковый радиус. Это означает, что их соответствующие точки на окружности равноудалены от центра.
Например, если окружность O конгруэнтна окружности P, это означает, что:
- Радиус окружности O равен радиусу окружности P
- Центр окружности O совпадает с центром окружности P
- Каждая точка на окружности O равноудалена от центра окружности O
- Каждая точка на окружности P равноудалена от центра окружности P
Пример 4. Конгруэнтные углы
Конгруэнтные углы — еще один тип конгруэнтных фигур. Два угла равны, если они имеют одинаковую меру. Это означает, что они имеют одинаковую степень вращения.
Например, если угол ABC равен углу DEF, это означает, что:
- Мера угла ABC равна мере угла DEF
- Оба угла имеют одинаковую степень вращения
Викторина
- Что означает конгруэнтность двух фигур? Ответ: Две фигуры конгруэнтны, если они имеют одинаковый размер и форму.

- Могут ли две фигуры быть конгруэнтными, если они не одного размера? Ответ: Нет, две фигуры должны быть одного размера, чтобы быть конгруэнтными.
- Могут ли две фигуры быть конгруэнтными, если они имеют разную ориентацию? Ответ: Да, две фигуры могут быть конгруэнтными, даже если они имеют разную ориентацию или положение.
- Какой символ используется для обозначения конгруэнтности? Ответ: Символ, используемый для представления соответствия, представляет собой знак равенства с тильдой (~) сверху, например: ?.
- Какие свойства формы должны быть одинаковыми, чтобы она была конгруэнтной другой форме? Ответ: Размер и форма фигуры должны быть одинаковыми, чтобы она была конгруэнтна другой фигуре.
- Конгруэнтные фигуры идентичны или просто похожи? Ответ: конгруэнтные фигуры идентичны по размеру и форме, а не просто похожи.
- Могут ли негеометрические фигуры, например буквы, быть конгруэнтными? Ответ: Да, негеометрические фигуры, такие как буквы, могут быть конгруэнтными, если они имеют одинаковый размер и форму.


 Подробно этой темой занимаемся на курсе по распознаванию лжи.
Подробно этой темой занимаемся на курсе по распознаванию лжи.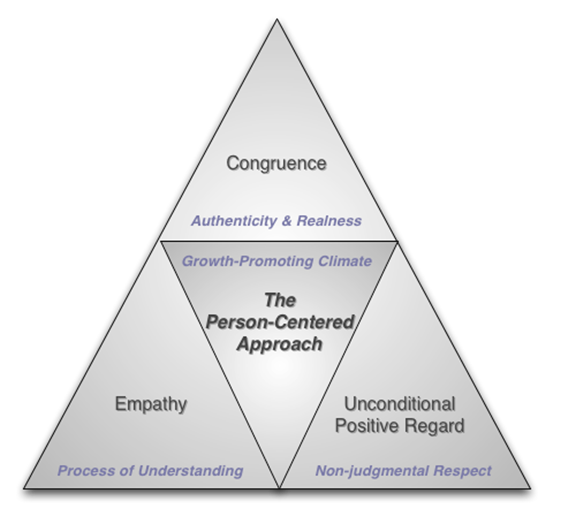 19.15 Фазовые равновесия и фазовые переходы
19.15 Фазовые равновесия и фазовые переходы V., Galenko, P. K. & Toropova, L. V., 2022, В: Crystals. 12, 12, 1686.
V., Galenko, P. K. & Toropova, L. V., 2022, В: Crystals. 12, 12, 1686. K., Toropova, L. V., Alexandrov, D. V., Phanikumar, G., Assadi, H., Reinartz, M., Paul, P., Fang, Y. & Lippmann, S., дек. 2022, В: Acta Materialia. 241, 118384.
K., Toropova, L. V., Alexandrov, D. V., Phanikumar, G., Assadi, H., Reinartz, M., Paul, P., Fang, Y. & Lippmann, S., дек. 2022, В: Acta Materialia. 241, 118384. V., Galenko, P. K. & Alexandrov, D. V., июл. 2022, В: Crystals. 12, 7, 965.
V., Galenko, P. K. & Alexandrov, D. V., июл. 2022, В: Crystals. 12, 7, 965. В треугольнике XYZ XY = 16 см, YZ = 13 см и ZX = 10 см. Два треугольника равны? Если да, то какой постулат вы использовали?
В треугольнике XYZ XY = 16 см, YZ = 13 см и ZX = 10 см. Два треугольника равны? Если да, то какой постулат вы использовали?